NMF: Non-negative Matrix Factorization（非負値行列因子分解）

id:naoyaさんがこちらでNon-negative Matrix Factorization(NMF)について説明していて，おもしろいと思ったので調べてみました．

NMFの概要

NMFとは非負値行列を2つの非負値行列に分解するアルゴリズムです．
こうすることで，もとの行列が持つ潜在的要素を明確に示すことができるというものです．
NMFは90年代中頃からあったアルゴリズムのようですが，広く知られるようになったのは[1]の論文がきっかけのようです．(Wikipediaより)

Learning the parts of objects by non-negative matrix factorization

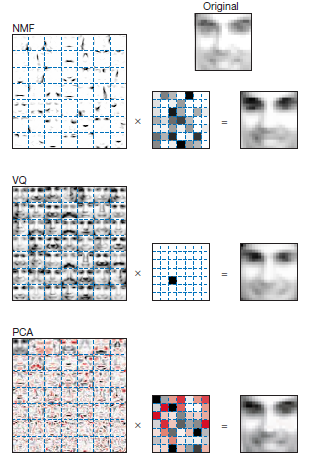
[1]ではm人の顔画像(n次元ベクトル)を表現する行列V(n x m)を \(V \approx WH\) (W: n x r, H: r x m)と分解しています．
Wの各列は基底画像(basis image)を表し，Hの各列はそれらの画像をどれだけの重みで結合するかを表します．
つまり，行列Hのi列目のベクトルを \(\bm{h}_i\) と表すと，i番目の人の顔画像 \(\bm{v}_i\) は

\[\bm{v}_i \approx \bm{W}\bm{h}_i\]

と表現されます．
この分解には主成分分析(PCA)，ベクトル量子化(VQ)，NMFを用いて比較しています．

下の図がr=49で分解した結果で，それぞれ結果が大きく異なります．（黒は正値，赤は負値を表します）
それぞれ，一番左の画像がW(49枚の基底画像)，真ん中が \(\bm{h}_i\)，右が \(\bm{v}_i\) となっています．

NMFの基底画像は顔の各パーツにわかれていることがわかるかと思います．
VQの基底画像はm人をr個のクラスタに分けた際の代表画像です．
PCAの基底画像は・・・なんかすごいことになってます．

NMFだとどうして局所的な特徴が抽出できるのか？

さて，どうしてNMFではこのように顔のパーツがはっきりと分かれるのでしょうか？

それは”非負値”であることがポイントです．
おそらくこのような結果になる理論的な説明はありません．（あれば教えてください）

例えば，この例のように様々な人の顔を少ない基底画像の重ね合わせ(足し算)で作成することを考えましょう．
具体的に，1000人の顔画像を50枚の基底画像(素材)で作成するとします．どのような素材が必要になりますか？
ここで重要なのが，NMFで分解した行列の重みが非負値であるように，素材を単純に追加する(足し合わせる)ことしかできないということです．
つまり，ある素材とある素材の差分をとるような複雑なことはできません．
（VQの基底画像で足し合わせたり差分をとったりできればかなりの顔が表現できそうです）

そうなると，１つの素材で顔を表現できすぎる場合(目やら鼻やら口やら・・・)，
素材を追加する時に競合してしまうので（目が4つになるなんてことも！），
１つの素材では顔の各パーツを表現するにとどめた方が良いことに気付くと思います．
アバターとかを作る場合に，目や鼻や口などが別々に用意されてますよね？あれです．

そんなわけで，NMFの結果は私たちの直感ともよく合うと言われています．
また，得られる行列がスパースであることも特徴です．
ちなみに \(\bm{h}_i\) は潜在意味変数とも表現されています．
どの基底画像を潜在的にどれだけ持っているのかを表現する変数ということだと思います．

自然言語処理への適用

[1]では他にも百科事典の索引語・文書行列（行は単語で列は文書）を分解することも試みており，
顔画像同様，Wの各列のベクトルは文書のトピックを表現するような単語により構成されたようです．
このように関連の強い単語をソフトクラスタリングしたりと，様々な用途に使えます．

ところで，Wの各列がいわゆる特徴というやつで，各値は対応する単語がその特徴(トピック)においてどれだけ重要かを表します．
Hの各行が特徴であり，各値は対応する文書がその特徴(トピック)においてどれだけ適合しているかを表します．¹

NMFの実装

NMFの実装は非常に簡単で，[2]ではそのことについて詳しく説明してくれています．
NMFはWとHの更新を繰り返すことで適した分解を行うのですが，
収束性や局所最適解の保証性などについても丁寧に証明してくれています．
途中のテーラー展開やイェンゼンの不等式には戸惑いましたが・・・．なぜその一言を説明してくれない！？

RだとNMFというパッケージがあるみたいです．→ http://cran.okada.jp.org/web/packages/NMF/
他にも実装している方がちらほらいます．→ http://lucille.sourceforge.net/blog/archives/000282.html，http://d.hatena.ne.jp/mjmania/20100317/1268806789

PCAについての補足

最後に，PCAの基底画像について補足しておきます．
PCAはご存知のとおり，分散を最大化させるような変換です．
パターン認識の感覚では，個人を特定するために個人の特徴をよく表す基底変換を施すものだと思うでしょう．（私はそうでした）
ところが，分散を最大化しているのはピクセルの値の分散です．
なので最初の基底画像(第1主成分)として顔画像のテンプレートのような画像がでてきます．

あと，PCAで思い出しましたが，「情報検索アルゴリズム」に

特異値分解と主成分分析のいずれも，データを表現するための最適な基底として自己相関行列の固有ベクトルを求めているのであり，両者は本質的に等価な技術であるということができる．

と書いてあるのですが，個人的にこの内容は誤りだと思います．さらには

特異値分解では，　ー中略ー　（変量の分散を最大にするという意味で）最適な基底となっている．

とまで書いてあります．主成分分析は変換後の変量の分散が最大化されるような変換行列（重みベクトル）を導出するとあのような形になるのであって，特異値分解にそのような導出過程があるとは思えません．（実際，変量の分散が最大にならない反例はいくらでも挙げられます．）
対象となる行列を中心化した上での特異値分解であれば主成分分析と等価なので，関連の強い技術というのであれば納得がいくのですが・・・．
その辺に詳しい方がいらっしゃればご教示お願いします．

参考文献

[1] D. D. Lee and H. S. Seung, Learning the parts of objects by non-negative matrix factorization, Nature, Vol. 401, No. 6755, pp. 788–791, 1999.
[2] D. D. Lee and H. S. Seung, Algorithms for Non-negative Matrix Factorization, In NIPS, Vol. 13, pp. 556-562, 2000.
[3] Toby Segran (著), 當山 仁健 , 鴨澤 眞夫 (翻訳), 集合知プログラミング, オライリージャパン, 2008

2011/2/16追記
「Rで学ぶクラスタ解析」の付録では更新式の展開が丁寧に説明されていたので，[2]を読んでもわからなければ目を通してみるとよいかもしれません．