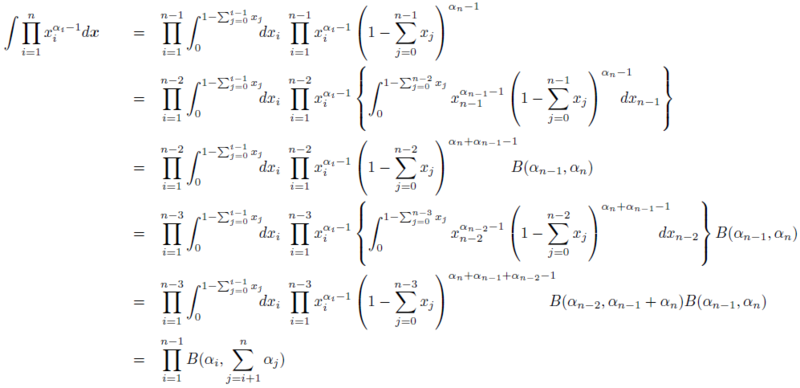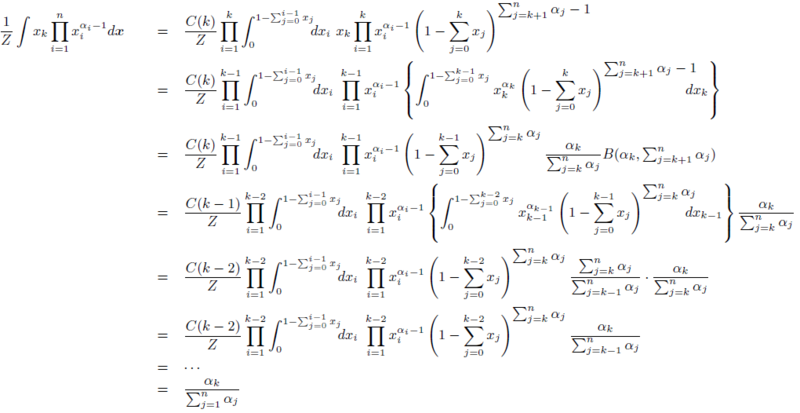ディリクレ分布まとめ

()

ディリクレ分布についていまいちイメージがつかなかったのでまとめてみました．
後半では正規化項，期待値，分散の算出過程を示しています．物好きな人は御覧ください．

どんな分布？

あるn個の事象についてi番目の事象が \(\alpha_i-1\) 回発生した場合に，その事象の生起確率が \(x_i\) である確率の分布です．
つまり，i番目の事象が \(\alpha_i-1\) 回発生したということで，各事象について生起確率を \(x_i\) (i=1,2,…,n) と定めると，それがどれだけ正しそうかの確率を返します．
ベータ分布について理解している人はベータ分布を多変量に拡張したものと考えるとわかりやすいです．

ディリクレ分布は以下の式で表されます．

\[p(\bm{x};\bm{\alpha})=\frac{1}{Z}\prod_{i=1}^n x_i^{\alpha_i-1}\hspace{10mm}\left(Z=\frac{\textstyle\prod_{i=1}^n \Gamma(\alpha_i)}{\Gamma(\textstyle\sum_{i=1}^n\alpha_i)}\right)\]

ここで，\(x_i\ge 0\)，\(\textstyle\sum x_i=1\)，\(\alpha_i > 0\) です．
ただし，\(\alpha_i=1\) の場合，\(x_i \ne 0\) でなければならないと思います．0の0乗が出てくるので．
\(x_i\) の期待値は

\[E[x_i] = \frac{\alpha_i}{\textstyle\sum_{j=1}^n\alpha_j}\]

分散は

\[\mathrm{var}[x_i] = \frac{\alpha_i\textstyle\sum_{j \ne i}\alpha_j}{(\textstyle\sum_{j = 1}^n\alpha_j)^2(1+\textstyle\sum_{j=1}^n\alpha_j)} = \frac{E[x_i]\left(1-E[x_i]\right)}{1+\textstyle\sum_{j=1}^n\alpha_j}\]

となります．

最初の説明だと \(\alpha_i-1\) は0以上の整数でなければならないので，もう少し違う解釈をすると，ある標本におけるi番目の事象の生起確率が \(\phi_i\) だった場合に重みγ（標本内での生起確率がどれだけ信頼できるか）を掛けた値が \(\alpha_i\) です．つまり \(\alpha_i=\gamma\phi_i\) です．
これで \(\alpha_i-1\) は-1より大きければ少数でも良いということになります．
ちなみに \(\phi_i\) は\(x_i\) の期待値でもあります．

以上の説明から，多項分布のパラメータ(各事象の生起確率)を定めたときに，ディリクレ分布はそのパラメータの妥当性を表すことになるので，多項分布の事前確率分布としてよく利用されます．
多項分布とディリクレ分布の積はディリクレ分布の形をするので，ディリクレ分布は多項分布の共役事前分布でもあります．（事後確率分布が事前確率分布と同じ関数形になる）

3変量で分布を可視化してみる

式だけ眺めていてもイメージがつきにくいので，3変量で実際にどのような分布になるのか表示してみます．
x3=1-x1-x2より，2次元にプロットすることができます．
グラフの色のデザインはこちら (PDF) をパクらせてもらいました．
（ただ，α < 1 の場合はうまく出力できませんでした・・・）
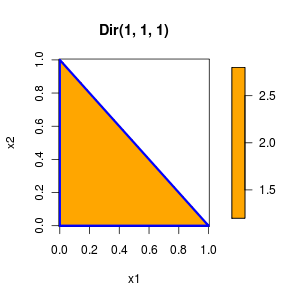
ディリクレ分布はDir(α1, α2, α3)という表記で表現しています．

20100401152952
20100401235721
20100401235720

α1=α2=α3=1のときは一様分布になります．
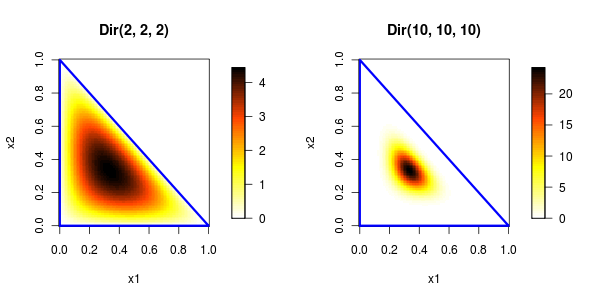
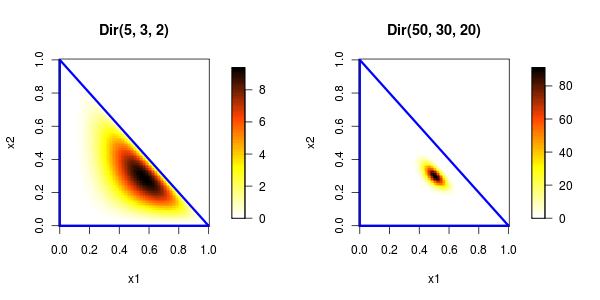
αの比，つまりα1:α2:α3が同じであっても，αが大きいほど分布が密集していることがわかると思います．
分散の式を見てみると，αの増加に従って，分子がαの2乗で増加するのに対し，分母がαの3乗で増加することがわかります．
よって，αが大きければ大きいほど分散は小さくなります．
ちなみに期待値の式からもわかるように，αの比が一緒であれば期待値も同じになります．

分布の特性から直感的に説明すると，標本数が大きければ大きいほど，その標本内での生起確率は信頼のおける値になります．
つまり，標本内での生起確率は母集団の生起確率である可能性が高くなります．
最初に説明したように，標本内の生起確率は期待値でもあるので期待値付近の密度が高くなります．

このサイトではαの値の変化に合わせて分布がどのように変化するかをアニメーションで表現しているので見てみるとおもしろいかもしれません．

画像の出力に使ったRのソースコードを以下に示します．

library(MCMCpack)
library(fields)

# Dirichlet distribution over three variables
dirichlet3d <- function(n = 25, alpha = rep(1, 3)){
  gx1 <- gx2 <- seq(0, 1, len = n)  # grid
  d <- outer(gx1, gx2, dirichlet3d.each, alpha)
  d <- ifelse(d != 0, d, NA)
  class(d) <- 'dirichlet3d'
  d
}

dirichlet3d.each <- function(x1_vec, x2_vec, alpha){
  mapply(function(x1, x2, alpha) ddirichlet(c(x1, x2, abs(1 - x1 - x2)), alpha),
         x1_vec, x2_vec, MoreArgs = list(alpha = alpha))
}

plot.dirichlet3d <- function(d, ...){
  dcolor <- colorRampPalette(c("white", "yellow", "orangered", "black"))(64)
  image.plot(d, col = dcolor, xlab = 'x1', ylab = 'x2', ...)
  polygon(c(0,1,0), c(0,0,1), border="blue", lwd=3)
}


alphas <- list(rep(1, 3), rep(2, 3), rep(10, 3), c(5, 3, 2), c(50, 30, 20))
for(i in 1:length(alphas)){
  png(sprintf("dirichlet%02d.png", i), width = 300, height = 300)
  plot(dirichlet3d(100, alphas[[i]]),
       main = sprintf("Dir(%d, %d, %d)", alphas[[i]][1], alphas[[i]][2], alphas[[i]][3]))
  dev.off()
}

正規化項，期待値，分散の算出

\({\{\bm{x}|\textstyle\sum_{i=1}^nx_i=1,\quad ^\forall x_i\ge 0\}},x_0=0\) とします．
また，\(\textstyle\int\!\!\int\!\!\int \!\!f(\bm{x})dx_1dx_2dx_3=\int\! dx_1\int\! dx_2\int\! dx_3f(\bm{x})\) は \({\textstyle\prod}_{i=1}^3\textstyle\int dx_i f(\bm{x})\) と表記することにします．
\(B(\alpha,\beta)\) はベータ関数であり，\(B(\alpha,\beta)=\textstyle\int^1_0 x^{\alpha-1}(1-x)^{\beta-1}dx\) です．

正規化項

こちらを参考にしました．
参考というより，自分がわかりやすいように書き直したって感じです．

・準備
次の関係が成り立つことを証明します．

\[\int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha-1}\left(1-\sum_{i=0}^k x_i\right)^{\beta-1}dx_k = \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta-1}B(\alpha,\beta) \tag{1}\]

\(x_k=(1-\textstyle\sum_{i=0}^{k-1}x_i)h_k\) とおくと

\[\begin{eqnarray}&& \int^{1-\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha-1}\left(1-\sum_{i=0}^k x_i\right)^{\beta-1}dx_k\\&=& \int^{1}_0\left\{\left(1-\sum_{i=0}^{k-1}x_i\right)h_k\right\}^{\alpha-1}\left\{1-\sum_{i=0}^{k-1}x_i - \left(1-\sum_{i=0}^{k-1}x_i\right)h_k \right\}^{\beta-1}\left(1-\sum_{i=0}^{k-1}x_i\right) dh_k\\&=& \int^{1}_0\left(1-\sum_{i=0}^{k-1}x_i\right)^\alpha h_k^{\alpha-1}\left\{\left(1-\sum_{i=0}^{k-1}x_i\right)\left(1-h_k\right) \right\}^{\beta-1} dh_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta-1}\int^{1}_0 h_k^{\alpha-1}\left(1-h_k\right)^{\beta-1} dh_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta-1}B(\alpha,\beta)\end{eqnarray}\]

・正規化項の算出
式展開の途中で式(1)を利用しています．
20100401212208

\(B(\alpha,\beta)=\displaystyle\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\) より，ガンマ関数に書き直すと \(i=j\) の \(\Gamma(\beta)\) と \(i=j+1\) の \(\Gamma(\alpha+\beta)\) が分子と分母で相殺されるので

\[\int\prod_{i=1}^n x_i^{\alpha_i-1}d\bm{x} = \frac{\textstyle\prod_{i=1}^n \Gamma(\alpha_i)}{\Gamma(\textstyle\sum_{i=1}^n \alpha_i)}\]

期待値

分布の特性からすると，直感的に標本内での生起確率が母集団での生起確率になりそうな気がするので，期待値の式は納得のいく形になっているかと思います．

・準備１
次の関係が成り立つことを証明します．

\[\int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha}\left(1-\sum_{i=0}^k x_i\right)^{\beta-1}dx_k = \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}B(\alpha,\beta)\frac{\alpha}{\alpha+\beta}\hspace{10mm}(k=1,2,\cdots) \tag{2}\]

正規化項の準備と同様にすると

\[\begin{eqnarray} && \int^{1-\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha}\left(1-\sum_{i=0}^k x_i\right)^{\beta-1}dx_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}\int^{1}_0 h_k^{\alpha}\left(1-h_k\right)^{\beta-1} dh_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}B(\alpha,\beta)\frac{1}{B(\alpha,\beta)}\int^{1}_0 h_kh_k^{\alpha-1}\left(1-h_k\right)^{\beta-1} dh_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}B(\alpha,\beta) E[h_k] \\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}B(\alpha,\beta) \frac{\alpha}{\alpha+\beta} \end{eqnarray}\]

・準備２
次の関係が成り立つことを証明します．

\[\int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha-1}\left(1-\sum_{i=0}^k x_i\right)^{\beta}dx_k = \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}B(\alpha,\beta)\frac{\beta}{\alpha+\beta}\hspace{10mm}(k=1,2,\cdots) \tag{3}\]

準備１と同様に

\[\begin{eqnarray}&& \int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha-1}\left(1-\sum_{i=0}^k x_i\right)^{\beta}dx_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}\int^{1}_0 h_k^{\alpha-1}\left(1-h_k\right)^{\beta} dh_k\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}\int^{1}_0 h_k'^{\beta}\left(1-h_k'\right)^{\alpha-1} dh_k'\hspace{10mm}\left(h_k = 1 - h_k'\right)\\&=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta}B(\alpha,\beta) \frac{\beta}{\alpha+\beta}\\ \end{eqnarray}\]

・準備補足
ベータ分布の期待値の求め方について補足しておきます．
ここの証明をちょっと変えています．

\[\begin{eqnarray} E[x] &=& \frac{1}{B(\alpha,\beta)} \int^1_0 x^\alpha(1-x)^{\beta-1}dx\\ &=& \frac{1}{B(\alpha,\beta)} \left\{\left[-\frac{1}{\beta}x^{\alpha}(1-x)^\beta\right]^1_0+\frac{\alpha}{\beta}\int^1_0 x^{\alpha-1}(1-x)^\beta dx\right\}\\ &=& \frac{\alpha}{\beta B(\alpha,\beta)} \int^1_0 x^{\alpha-1}(1-x)^{\beta-1}(1-x) dx\\ &=& \frac{\alpha}{\beta B(\alpha,\beta)} \left\{\int^1_0 x^{\alpha-1}(1-x)^{\beta-1} dx - \int^1_0 x^{\alpha}(1-x)^{\beta-1} dx\right\}\\ &=& \frac{\alpha}{\beta} \left\{1 - \frac{1}{B(\alpha,\beta)} \int^1_0 x^{\alpha}(1-x)^{\beta-1} dx\right\}\\ &=& \frac{\alpha}{\beta}\left(1 - E[x]\right) \end{eqnarray}\]

よって

\[E[x] = \frac{\alpha}{\alpha+\beta}\]

・期待値の算出

\(x_k(k \ne n)\) の場合，途中までは正規化項の算出と全く同じように計算することができます．

\(C(k)=\textstyle\prod_{i=k+1}^{n-1}B(\alpha_i,\textstyle\sum_{j=i+1}^n \alpha_j)\) とし，\(x_i\) の積分を行うと

20100401212209

途中の展開で式(2)，(3)を利用しています．

\(x_k(k = n)\) の場合も同様に計算することができます．

分散

・準備１
ベータ分布 \(\frac{1}{B(\alpha,\beta)}x^{\alpha-1} (1-x)^{\beta-1}\) において \(x^2\) の期待値が以下で表されることを証明します．

\[E[x^2] = \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)} \tag{4}\]

ここの証明をちょっと変えています．

\[\begin{eqnarray} E[x^2] &=& \frac{1}{B(\alpha,\beta)}\int_0^1 x^{\alpha+1} (1-x)^{\beta-1} dx\\ &=& \frac{1}{B(\alpha,\beta)} \left\{\left[-\frac{1}{\beta}x^{\alpha+1}(1-x)^\beta\right]^1_0+\frac{\alpha+1}{\beta}\int^1_0 x^{\alpha}(1-x)^\beta dx\right\}\\ &=& \frac{\alpha + 1}{\beta B(\alpha,\beta)} \int^1_0 x^{\alpha}(1-x)^{\beta-1}(1-x) dx\\ &=& \frac{\alpha + 1}{\beta B(\alpha,\beta)} \left\{\int^1_0 x^{\alpha}(1-x)^{\beta-1} dx - \int^1_0 x^{\alpha+1}(1-x)^{\beta-1} dx\right\}\\ &=& \frac{\alpha+1}{\beta} \left(E[x] - E[x^2]\right)\\ &=& \frac{\alpha(\alpha+1)}{\beta(\alpha+\beta)} - \frac{\alpha+1}{\beta}E[x^2]\end{eqnarray}\]

よって

\[E[x^2] = \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)}\]

・準備２
式(4)を使って次式を証明します．

\[\int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha+1}\left(1-\sum_{i=0}^k x_i\right)^{\beta-1}dx_k = \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta+1}B(\alpha,\beta)\frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)}\hspace{10mm}(k=1,2,\cdots) \tag{5}\]

正規化項の準備と同様にすると

\[\begin{eqnarray}&& \int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha}\left(1-\sum_{i=0}^k x_i\right)^{\beta-1}dx_k\\ &=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta+1}\int^{1}_0 h_k^{\alpha+1}\left(1-h_k\right)^{\beta-1} dh_k\\ &=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta+1}B(\alpha,\beta)\frac{1}{B(\alpha,\beta)}\int^{1}_0 h_k^2 h_k^{\alpha-1}\left(1-h_k\right)^{\beta-1} dh_k\\ &=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta+1}B(\alpha,\beta) E[h_k^2] \\ &=& \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta+1}B(\alpha,\beta) \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)}\\ \end{eqnarray}\]

同様に

\[\int^{1-\textstyle\sum_{i=0}^{k-1}x_i}_0 x_k^{\alpha-1}\left(1-\sum_{i=0}^k x_i\right)^{\beta+1}dx_k = \left(1-\sum_{i=0}^{k-1}x_i\right)^{\alpha+\beta+1}B(\alpha,\beta)\frac{\beta(\beta+1)}{(\alpha+\beta)(\alpha+\beta+1)}\hspace{10mm}(k=1,2,\cdots) \tag{6}\]

・準備３
式(5),(6)を踏まえて期待値の算出と同様に式展開すると

\[E[x_k^2] = \prod_{i=1}^{n-1}\int_0^{1-\textstyle\sum_{j=0}^{i-1}x_j} \!\!\! dx_i x_k^2\prod_{i=1}^{n-1}x_i^{\alpha_i-1}\left(1-\sum_{j=0}^{n-1}x_j\right)^{\alpha_n-1} = \frac{\alpha_k(\alpha_k + 1)}{\sum_{i=1}^n \alpha_i \left(\textstyle\sum_{j=1}^n \alpha_j + 1\right)}\]

・分散の算出

\[\begin{eqnarray} \mathrm{var}[x_k] &=& E[x_k^2] - \left(E[x_k]\right)^2\\ &=& \frac{\alpha_k(\alpha_k + 1)}{\left(\textstyle\sum_{i=1}^n \alpha_i\right) \left(\textstyle\sum_{j=1}^n \alpha_j + 1\right)} - \left(\frac{\alpha_k}{\textstyle\sum_{j=1}^n \alpha_j}\right)^2\\ &=& \frac{\alpha_k(\alpha_k + 1)\textstyle\sum_{j=1}^n \alpha_j - \alpha_k^2\left(\textstyle\sum_{j=1}^n \alpha_j + 1\right)}{\left(\textstyle\sum_{j=1}^n \alpha_j\right)^2 \left(\textstyle\sum_{j=1}^n \alpha_j + 1\right)}\\ &=& \frac{\textstyle\sum_{j \ne k}^n \alpha_j}{\left(\textstyle\sum_{j=1}^n \alpha_j\right)^2 \left(\textstyle\sum_{j=1}^n \alpha_j + 1\right)} \end{eqnarray}\]

参考