F値に調和平均を使う理由（再）

2010-11-21

(

)

正確にはF₁値と言うべきでしょうか．
以前F値に調和平均を使う理由というエントリーで苦しい説明をしましたが，もうちょっとうまい説明が思いついたのでまとめてみました．

検索結果の評価指標に適合率 (precision) と再現率 (recall) があります．
適合率は目的に合った文書（適合文書）が検索結果にどれだけ含まれているかという正確性の指標，
再現率は検索対象としている文書群の中に存在する適合文書のうちどれだけ検索結果に含まれているかという網羅性の指標です．

つまり，

U: 検索対象文書群の文書の数
R: 検索結果に含まれる適合文書の数
N: 検索結果に含まれる文書の数
C: 検索対象文書群に存在する適合文書の数

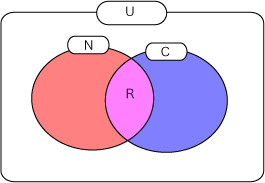
引用: 情報検索 - Wikipedia

とすると，

適合率 (precision) = R / N
再現率 (recall) = R / C

です．
検索結果に含まれる文書が多くなれば再現率は当然上がりますが，その分不必要な文書も増える可能性があるので，適合率は下がる傾向にあります．
このように適合率と再現率はトレードオフの関係にあるので，2つの指標をまとめたような指標としてF値があります．

F₁値は適合率と再現率の調和平均であり，

$F_1-score\hspace{10} =\hspace{10}\frac{2}{\frac{1}{precision}+\frac{1}{recall}}\hspace{10}=\hspace{10}\frac{2precision\cdot recall}{precision + recall}\hspace{10}=\hspace{10}\frac{R}{\frac{1}{2}(N+C)}$

で表されます．

っで，どうしてF₁値に相加平均じゃなくて調和平均を使うかです．
その前にまずは調和平均について理解を深めましょう．

調和平均の例

100 km の道のりを往復するのに，行きは 10 km/h で10時間，帰りは 100 km/h で1時間かかりました．
平均速度はいくつになるでしょうか？

「10 km/h と 100 km/h だから（相加）平均すると 55 km/h だ！」

おいおい，10 km/h では10時間も走行してるのに，100 km/h では1時間しか走行してないんだからなんか違わないか？

11時間かけて200 km 移動しているので約18 km/h ですね．
さすがにこれほど極端だと相加平均を取る人はいないかと思います．

でもこの問題を次のように変えるとどうでしょうか？

同じ道のりを行きは a km/h，帰りは b km/h で走行しました．平均速度はいくつになるでしょうか？

(a + b) / 2 と答えたくなりませんか？

この問題は往復 2x km の移動という課題を達成するのに，行きは x / a 時間というコスト，帰りは x / b 時間というコストをかけているわけです．
つまり (x /a + x / b) 時間かけて 2x km 移動しているわけです．
平均速度を求める式は

$\frac{2x}{\frac{x}{a} + \frac{x}{b}} = \frac{2}{\frac{1}{a} + \frac{1}{b}}$

これが正に調和平均です．

調和平均は同じ課題 x を達成するのに効率 a と効率 b で行った場合の平均効率といった捉え方をするといいんじゃないでしょうか．
これは2つの効率でこなした課題 2x を全体のコストで割った効率ということになります．

だからF₁値は調和平均なのか！

情報検索と言えば，やっぱり適合文書を抽出したいですよね．
じゃあ情報検索における課題は適合文書を x 個抽出することだとしましょう．

情報検索には2つの効率が存在します．適合率と再現率です．

検索対象の文書が全部で100個ありました．その中に適合文書は1個だけ存在します．
また，どんな検索対象に対しても適合率0.1，再現率1の検索エンジンがあります．
この検索エンジンで検索してみると，確かに検索結果に含まれる文書の数は10個で，適合文書は1個ありました．
検索エンジンの適合率と再現率の平均はいくつでしょう？

※適合文書数と検索対象の文書数の比が1/10より大きい場合はそもそも適合率0.1に成り得ないとか言わないでくださいね

「適合率は0.1で，再現率は1だから（相加）平均は0.55だ！」

なんか違う気がしますよね．とりあえず相加平均を使うのは違うよなぁといった感じです．
ちなみに調和平均は約0.18になります．

ここで見落としているのは，かかっているコストが適合率と再現率で違うことであり，

適合文書を x 個抽出するのが課題であるということ
適合率と再現率が効率だということ
それぞれの効率にとってのコストが何であるかということ
を明確にしなければなりません．

まず再現率にとってのコストは何でしょうか？
それは検索対象の文書群に存在する適合文書の数です．
たとえ再現率が1であってもそもそも適合文書が x個存在しなければ課題が達成できません．
再現率が0.1の場合は10x個も存在しなければならないのです．

じゃあ適合率にとってのコストは何でしょうか？
それは検索結果に含まれる文書数です．
たとえ適合率が1であっても x個の文書を抽出してこなければ課題が達成できません．
適合率が0.1の場合は10x個も抽出してこなければならないのです．

これらのコストは必要な文書数ということで同様に扱ってしまいましょう．
そうすると平均速度の問題とのアナロジーが取れます．

	平均速度	F₁値
課題	x km の移動	x 個の適合文書の取得
効率1	行きの速度 a km/h	適合率 a
コスト1	かかった時間 x / a 時間	必要な文書数 x / a （検索結果の文書数）
効率2	帰りの速度 b km/h	再現率 b
コスト2	かかった時間 x / b 時間	必要な文書数 x / b （検索対象に含まれる適合文書の数）

情報検索の先ほどの問題でなんか違うなぁと感じたのは
「おいおい，適合率0.1だから10個も文書を抽出しているわけで，再現率が1でも適合文書はそもそも1個しかないんだからなんか違わないか？」
という感覚かなぁと思います．コスト（必要な文書数）が違うのです．普通なら因果関係が逆な気もしますが…

最初に説明したように適合率と再現率はトレードオフの関係にあるので往復の平均速度の問題と比べると複雑ですし，
そもそも適合率も再現率も現実的に一定ではないので無理はあるんですがね…
まぁそれを言い出すと速度一定も現実的にはありえないわけですし……

とにかく，
調和平均は同じ課題を異なる効率でこなす場合の平均効率であり，適合率も再現率も適合文書を得るための効率
だと考えればF₁値として調和平均をとることもしっくりこないでしょうか？

調和平均の例

だからF1値は調和平均なのか！

だからF₁値は調和平均なのか！