Latent Dirichlet Allocation (LDA) ゆるふわ入門

2013-03-12

(

)

NLP 2013 の時期ですね。たぶんギリギリ NLPer の端くれの端くれの身としては参加したい気持ちも山々なのですが、いろいろあって今年は参加しないことにしました。
NLP 2014 は参加しようと思うので来年はかまってやってください。

ときに、私が NLP を勉強し始めた頃はかな漢字変換や音声認識で文脈を考慮して推定したいなぁみたいなことを考えていたので言語モデル、中でもトピックモデルに興味を持っていました。
っで、トピックモデルと言ったら Latent Dirichlet Allocation (LDA) じゃないですか？Blei 先生の論文読むじゃないですか？意味不明じゃないですか！？
そもそもディリクレ分布って何？な人だったので・・・。ディリクレ分布まとめ - あらびき日記とかその時の痕跡ですね。

PRML の上巻を読んでちょっとベイズな考え方に慣れて LDA も理解できてきたと思い輪講で LDA を紹介したら、変分近似のところで「それって平均場近似だよね？」とか突っ込まれて「あ、はい、なんか、そう、言われて、ます、ね・・・（平均場近似が何なのかよくわかってないけど）」となったこともあり、LDA は自分には到底理解できないものだと思ったものです。
cf. 独立性の仮定と平均場近似の関係 - あらびき日記

前置きが長くなりました。
最近 LDA を勉強していてようやく論文の内容がわかった気がしたので 3 年前の自分に向けてゆるふわに LDA を解説しようと思います。
基本的に論文 [1] に対するざっくりとした解説です。

LDA とは何ぞや？

LDA は1つの文書が複数のトピックから成ることを仮定した言語モデルの一種です。
日本語だと「潜在的ディリクレ配分法」と呼ばれます。単語などを表層的と表現するならば、トピックは単語と違って表面には現れないので潜在的です。その潜在的な要素の分布の事前分布にディリクレ分布を仮定してごにょごにょするから「潜在的ディリクレ配分法」と呼ぶのかなぁと思ってます。

LDA による文書の生成過程は次の通りです。

単語数 N を選択 $N \sim \rm Poisson(\xi)$
トピックの確率分布（多項分布のパラメータθ）を選択 $\Theta \sim \rm Dir(\alpha)$
N 個の単語それぞれに対して
(a) トピック z_n をトピックの確率分布に従って選択 $z_n \sim \rm Multinomial(\Theta)$
(b) トピック z_n に対する単語の確率分布に従って単語 w_n を選択 $p(w_n\|z_n,\mathbf\beta)$

単語数 N がポアソン分布に従うという仮定については、もっと適切な分布があるはずだけどとりあえず、みたいな感じらしいので気にしなくて良いです。
トピックの多項分布パラメータθはディリクレ分布に従うことを仮定します。ディリクレ分布はざっくりと説明すると確率分布の確率分布です。例えば、3つのトピック「スポーツ」、「経済」、「政治」があったとして、各トピックの生成確率 (スポーツ、経済、政治) = (0.3, 0.2, 0.5) になる確率は 0.1、(スポーツ、経済、政治) = (0.1, 0.2, 0.7) になる確率は 0.2 のように確率分布の確率を定めます。
トピックの生成確率は多項分布を仮定します。例えば、「スポーツ」の生成確率は 0.3、「経済」の生成確率は 0.2 のように定義します。¹
単語の生成確率も多項分布を仮定します。この多項分布はトピックによって変わります。
なお、トピックの数は適当な数が与えられるものとします。

上記過程をグラフィカルモデルで表したのがお馴染みの次の図です。([1] の Fig. 1)

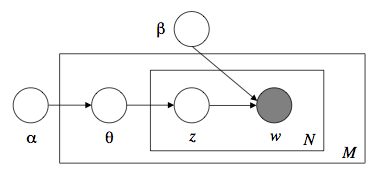
以上より、コーパス（全対象文書）の生成確率は次のように表されます。
$\displaystyle p(D\|\alpha, \beta) = \prod^M_{d=1}\int p(\theta_d\|\alpha)\left(\prod^{N_d}_{n=1}\sum_{z_{d_n}}p(z_{d_n}\|\theta_d)p(w_{d_n}\|z_{d_n},\beta)\right)d\theta_d$

観測できているのは単語だけなので、トピックなど非観測なものは全ての可能性を考慮して積分したり総和を取ったりしています。

LDA における推論

Wikipedia には推論の説明として次のように載っています。

推論（すいろん、英語: inference, reasoning）とは、既知の事柄を元にして未知の事柄について知ろうとすることである。

LDA において既知の事柄とは何か？どの単語が生成されたかですね。
未知の事柄とは何か？それらの単語がどのトピックから生成されたかですね。

というわけで、LDA における推論は次の事後確率分布を求めることになります。
文書（w の集合）が与えられた時のトピックの選択確率と、各単語がどのトピックから生成されたかに関する確率分布です。
$\displaystyle p(\theta, \mathbf{z}\|\mathbf{w}, \alpha, \beta) = \frac{p(\theta, \mathbf{z}, \mathbf{w} \| \alpha, \beta)}{p(\mathbf{w} \| \alpha, \beta)}$

ところが、上式の分母は次のようにθの積分と z の総和があり、こんなのとても計算できません。
$\displaystyle p(\mathbf{w}\|\alpha, \beta) = \int p(\theta\|\alpha)\left(\prod^N_{n=1}\sum_{z_n}p(z_n\|\theta)p(w_n\|z_n,\beta)\right)d\theta$

この問題に対処するために変分ベイズ [1] や MCMC [2] によって分布を近似する手法が提案されています。
[2] については id:n_shuyo さんの Latent Dirichlet Allocations の Python 実装 - Mi manca qualche giovedi`? が参考になると思います。

p(w|α,β) はとても計算できるような分布じゃないので p(θ,z|w,α,β) も計算出来ません。よって、より簡単な次のような分布で近似します。²
$\displaystyle q(\theta,\mathbf{z}\|\gamma,\phi)=q(\theta\|\gamma)\prod^N_{n=1}q(z_n\|\phi_n)$

q(θ|γ) がディリクレ分布（パラメータ数はトピック数と同じ）、q(z|φ) が多項分布（パラメータ数は単語数 x トピック数、または語彙数 x トピック数）です。
あとは p(w|α,β) をよく近似する q(θ,z|γ,φ) が求まればそれなりに正しい結果が得られます。
つまり、文書を与えてやるとその文書の各単語がどのトピックから生成されたかに関する確率分布が得られるわけです。近似値ですが。
q(θ,z|γ,φ) を求めるためにコーパスに対する尤度が大きくなるようなγとφを求めることになるんですが、尤度については後で出てくるんで一旦置いときます。

LDA におけるモデル選択

LDA の文書生成過程や推論の説明ではαやβについてあまり触れていませんでした。
αはトピックの選択確率を得るためのパラメータで、βはトピックに応じて単語の生成確率を得るためのパラメータです。
この2つのパラメータが言語モデルとしての LDA を特徴付けるのに重要な役割を果たしています。

っで、これらのパラメータを決定するのに既存のコーパスに対する尤度を最大化すればそのコーパスに対して最良のα、β、つまり最良のモデルを選択することができますよね。
よって、次の尤度関数を最大化すれば良いことになります。
$\displaystyle l(\alpha, \beta) = \sum_{d=1}^M \log p(\mathbf{w}_d\|\alpha,\beta)$

ところが、前述したように p(w|α,β) は計算できないので、先ほど近似した q(θ,z|γ,φ) を使います。

「？？？」って感じですよね。
ところが、あら不思議、Jensen の不等式を用いることで次のように log p(w|α,β) の下限値を定めることができちゃいます。（[1] の式12）
$\displaystyle \log p(\mathbf{w}\| \alpha, \beta) \ge \int \sum_{\mathbf{z}} q(\theta,\mathbf{z}\|\gamma,\phi) \log p(\theta, \mathbf{z}, \mathbf{w} \| \alpha, \beta) d\theta$ $\displaystyle- \int \sum_{\mathbf{z}} q(\theta,\mathbf{z}\|\gamma,\phi) \log q(\theta,\mathbf{z}\|\gamma,\phi) d\theta$

さらにはこの下限値は [1] の式 15 に表わされるように解析的に解くことができるので³、最大化するα、βも簡単に求まります。

ここで問題が出てきます。
αとβを求めるのに q(θ,z|γ,φ) を利用するということはγとφが求まっていなければなりません。
ところがγとφを求めるにはαとβ必要です。cf. [1] の式 6, 7

なので、

適当なαとβを定める
現在のαとβに対して各文書における最良のγとφを求める (E-Step)
現在のγとφに対して最良のαとβを求める (M-Step)
収束するまで 2, 3 を繰り返す

という手順が必要です。変分ベイズ法とかいうシャレた名前がついていますが、何てことはない EM アルゴリズムです。
どっちも Maximization じゃないかという気もしますが、EM アルゴリズムらしいです。
αとβはコーパスに対して1つ定まるパラメータで、γとφは文書ごとに定まるパラメータであることも注意してください。

結局 LDA って何に使えるの？

まず、言語モデルとしては pLSI などに比べて perplexity 的に良くなる（perplexity が低くなる）ことが多いらしいです。
perplexity は次の式で表されますが、変分ベイズによる LDA の場合は log p(w) を前述の下限値で置き換えているんじゃないかと思います。⁴
$perplexity(D_{test})=\exp\left{-\frac{\sum_{d=1}^M\log p(\mathbf{w}_d)}{\sum_{d=1}^M N_d}\right}$

文書クラスタリングなんかにも使えます。
推論の際に各文書に対してγとφを求めました。
中でも、γはトピックの選択確率を定めるものなので、その文書がどのようなトピックから構成されるものかを特徴付けるパラメータです。
つまり、同じようなトピックから成る文書は同じクラスタに属するようにしたいといった用途であればこのパラメータを特徴量に使うことができます。
単語の出現回数を特徴量に取ると語彙数の膨大な次元になってしまいますが、γを特徴量に取るとトピック数という比較的小さな次元で比較することができます。
さらには、単語の出現回数を特徴量に取ると潜在的意味だと同じだけど表層的に違うと類似度は下がってしまいます。例えば「車」と「自動車」は同じように扱いたいですよね。LDA だと「車」という表現を使っている文書も「自動車」という表現を使っている文書もトピック的に同じであれば同じように扱うことが可能です。

αとβさえ与えてやれば未知の文書に対してもγとφを求めることができるのも良いですよね。

あとは協調フィルタリングにも使えたりと、まぁ応用分野はいろいろありますよね。
画像処理なんかにも使われるみたいですし。

雑感（個人的なメモ） (2013-03-13 追記)

論文を読んでると、q(θ,z|γ,φ) が出てきたり、文書クラスタリングのところでγが使われていたりと、よく理解しないで読んでいると LDA の学習（モデル選択）とはγを求めることなのだと勘違いしてしまうかもしれません。

あくまで学習はαとβを求めることです。
LDA の推論によって各文書を特徴付けるγが出てきます。
しかしγやφを最適化するために使う尤度を表現する上でα、β、γ、φが出てくるので、αとβがしっかり定まっていない場合は推論とモデル選択を交互に行い収束するまで最適化を繰り返すことになります。
既に何らかのコーパスでαとβを学習していれば（そのコーパスでは推論したくなくても各文書に対してγ、φを求めることになりますが）、推論したい初見の文書が与えられても学習済みのαとβを使うことでγとφを1回の最適化で求めることができます。

また、p(θ,z|w,α,β) は q(θ,z|γ,φ) で近似したけど p(w|α,β) を近似していないから perplexity なんか計算できない！どうやって perplexity を計算してるんだ！と思うかもしれませんが q(θ,z|γ,φ) を導入することで perplexity の下限値を解析的に解くことができるようになります。
この辺は論文の本文中にはさらっと書かれているだけで数式自体は Appendix にしか出てこないのでつまづきポイントなのかなと思います。

参考

[1] D. Blei, A. Ng, and M. Jordan, “Latent Dirichlet Allocation”, in Journal of Machine Learning Research, 2003, pp. 1107-1135.
[2] T. L. Griffiths and M. Steyvers, “Findingscientific topics”, Proceedings of the National Academy of Science, 2004, pp. 5228-5235.

あと、LDA を理解するのに PRML はかなり良い文献になると思います。「これ、PRML で勉強したところだ！」ってなります。

Amazonで詳細を見る

おまけ～ LDA-C をピュア R に移植してみた～

理解を深めるために LDA-C をピュア R に移植してみたので一応晒しておきます。αの更新式がどうしても理解できません・・・。
https://github.com/abicky/lda-r

それっぽい結果にはなってますがバグってるかもしれないですし、めちゃくちゃ遅いので使う人はいないでしょうが、例えば次のように使います。

> source("lda.R")
> lda <- LDA$estimate("./ap/ap.dat")

以上、LDA についてのざっくりした解説でした！
各パラメータの更新式の導出についてはまたどこかでまとめようと思います。

多項分布というと n 回の試行に対して各事象が x1, x2, …, xk 回起こる確率の分布なわけですが、ここで言う多項分布は n = 1 なので少し困惑するかもしれません。つまり単語を選ぶという 1 回の試行に対してあるトピックが 1 つ割り当てられる確率です。 ↩
これが物理学で平均場近似と呼ばれる近似手法に対応するらしいですよ！ ↩
むしろ解析的に解ける形に持っていけるように Jensen の不等式を用いているわけですが ↩
R の topicmodels パッケージはそのようにして導出しています ↩