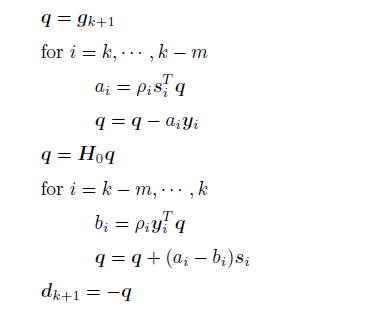L-BFGS法はだからメモリが節約できるのか!
L-BFGS法 は limited memory BFGS ということで,準ニュートン法をBFGS法に基づいて省メモリで実現する方法です.(その程度の理解度です…)
BFGS法による準ニュートン法の簡単な説明
準ニュートン法では,kステップ目のヘッセ行列の逆行列の近似行列を \(\bm{H}_k\) ,勾配を \(\bm{g}_k(=\nabla f(\bm{x}_k))\) とおくと,更新式は次のようになります.
\[\bm{x}_{k+1} = \bm{x}_k - \alpha_{k} \bm{H}_k \bm{g}_k\]ここで, \(\alpha_{k}\) は1次元探索によって決定するステップ幅です.
BFGS法では \(\bm{s}_k = \bm{x}_{k+1} - \bm{x}_k,\hspace{5mm}\bm{y}_k = \bm{g}_{k+1} - \bm{g}_k\) とおくと \(\bm{H}_k\) を次のように更新します.
この更新には \(\bm{H}_k\) を保持しておく必要があるので, \(\bm{x}\) の次元数をnとすると \(\bm{O(n^2)}\) のメモリ領域を必要とします.
L-BFGS法による準ニュートン法
\(\bm{V}_k = \bm{I} - \rho_k\bm{y}_k\bm{s}_k^T, \rho_k = 1/\bm{y}_k^T\bm{s}_k\) とおくと,先ほどの更新式は
\[\bm{H}_{k+1} = \bm{V}_k^T \bm{H}_k \bm{V}_k + \rho_k\bm{s}_k\bm{s}_k^T\]と表され, \(\bm{H}_k\) を再帰的に展開すると
\[\begin{eqnarray} \bm{H}_{k+1} &=& \nonumber\left(\bm{V}_k^T\cdots \bm{V}_0^T\right)\bm{H}_0 \left(\bm{V}_0\cdots \bm{V}_k\right)\\\nonumber&+& \rho_0\left(\bm{V}_k^T\cdots \bm{V}_1^T\right)\bm{s}_0 \bm{s}_0^T\left(\bm{V}_1\cdots \bm{V}_k\right)\\\nonumber&+& \rho_1\left(\bm{V}_k^T\cdots \bm{V}_2^T\right)\bm{s}_1 \bm{s}_1^T\left(\bm{V}_2\cdots \bm{V}_k\right)\\\nonumber&& \vdots\\&+& \rho_k \bm{s}_k \bm{s}_k^T\end{eqnarray}\]となります.この更新式はヘッセ行列の逆行列の近似行列の初期値(普通は単位行列などのスパースな行列) \(\bm{H}_0\) と,現在と過去全てのステップの \(\bm{x}\) と \(\bm{g}\) から算出できるベクトルから構成されているので,これらを保持しておくための \(O(kn)\) のメモリ領域しか必要としません.
これだとBFGS法をちょっと工夫しただけなのですが,L-BFGS法では過去のmステップ分の \(\bm{x}\) と \(\bm{g}\) しか保持しておきません.(m は普通10以下だとか)
よって,
とします.これで必要なメモリ領域は \(O(mn)\) となります.ちなみにこれはある程度更新を繰り返した k > m の場合です.
ここで注意しなければならないのは,上の更新式は \(\bm{H}_{k+1}\) そのものを計算するためのものではなく,探索方向 \(\bm{d}_{k+1} = - \bm{H}_{k+1} \bm{g}_{k+1}\) を求めるための \(\bm{H}_{k+1}\) の定義だということです.結局求めたいのは探索方向 \(\bm{d}_{k+1}\) であり,上式に右から \(\bm{g}_{k+1}\) を掛けることで次のように逐次的に求めることができます.
上記の逐次計算では \(\bm{H}_0\) を除いてn次元ベクトルしか出てこないのがポイントです.そして \(\bm{H}_0\) がスパースな行列であるということが前提です.
最初にL-BFGS法を見たときは,結局 \(\bm{H}_{k+1}\) を計算したら \(O(n^2)\) のメモリ領域が必要じゃん!と思ったのですが, \(\bm{H}_{k+1}\) を求めることなく探索方向をこんな鮮やかに計算できるんですね….
上記逐次計算の巧妙さに感動しました.
しかしBFGS法ではどういう過程で \(\bm{H}_{k}\) の更新式が導出されたのかが気になる…
参考文献
- Dong C. Liu, Jorge Nocedal, Dong C. Liu, Jorge Nocedal. On the limited memory BFGS method for large scale optimization. Mathematical Programming, Vol 45, pp. 503-528, 1989
- L-BFGS, Wikipedia